Masonry Arches, Shapes and Forces






Pointed arches have a profile that is slightly closer to a catenary shape than a semicircular one; therefore, the limit-thickness is a little thinner for a given span. This implies the need for a little less buttressing.
The Etruscans, The Romans and the ancient Chinese dynasties all successfully built masonry arch bridges with no knowledge of catenary curves. While many Roman bridges remain intact across Southern Europe, no surviving standing examples exist in Scotland or England. Arch building became a lost art for 600 years but re-emerged in the early 12th-century. Rare surviving examples of Norman (Romanesque) vaulted stone bridges include the Fountains Abbey Infirmary Bridge in Yorkshire and the Clattern Bridge in Kingston. These ancient vaulted bridges have rounded arches in the Roman tradition. No Norman period bridges survive in Scotland. Romanesque architecture was largely overtaken by pointed Gothic architecture in the 13th century, although there were also many semicircular and segmental structures in this period, and a few elliptical shapes, most of them requiring buttressing. Then, in the 16th-century, the Gothic style disappeared quite quickly due to a combination of Renaissance influence and Reformation zeal. Rounded arches predominated thereafter.
The catenary principle has been understood for several hundred years, so why do we see so few catenary-shaped arches? The problem is that a catenary shape for bridges is less practical than a rounded one, and more expensive, because the radius of the curve varies smoothly through the arc, and each voussoir needs an individually tailored template (circular arch voussoirs are all the same shape.) It was more effective and cheaper to use loading and buttressing of abutments to manoeuvre the geometry to match an expected limit force-line. Moreover, there was a strong precedent to follow. Roman and medieval masons had excelled in this area despite lacking modern engineering concepts. They had extensively developed empirical geometric rules for determining appropriate arch and abutment thicknesses relative to span. It is now being discovered that the stabilising and strengthening effects of the backfill have contributed much more than was thought to the survival of these old structures.

The most suitable shape for a dome is also a catenary and it is interesting that Inuit igloos appear mostly to be of that shape. Could it be that the ephemeral nature of the building-material fostered many rebuilds and an early empirical solution?
Stone is extremely strong under compression but very weak in tension, so masonry structures must be designed to avoid stretching or bending forces. Compression-only is the rule for unreinforced masonry design and this is achieved by ensuring the gavitational thrust line stays within the body of the masonry. The design of arches, therefore, must ensure that the force-line is directed outward and downward within the arch stones (voussoirs). In this way tension-stress is avoided, and once this condition is met, the material strength of the stone becomes less important.
A freestanding arch subjected to uniform loading generates a force-line that follows a catenary curve—a mathematical function represented by the shape of an inverted hanging chain. This principle was first outlined, in 1675, by Robert Hooke. Catenaries form a family of curves, where the profile depends on the tightness of the chain. It follows that If the force-line must remain within the arch, it would seem generally sensible to construct arches in a catenary shape.
However, any shape is viable, provided that the thickness (between the intrados and extrados) is sufficient to accommodate at least one catenary line. As early as 1697, Gregory (Ref) had observed that “when an arch of any other figure is supported, it is because within its thickness some catenaria is included.” The force-line does not need to be real or actual; it only needs to be possible. If it exists, the structure will find it and remain safe.

As an example, the semicircular arch in this sketch has been made increasingly thinner by increments until a point was reached where only one catenary line would fit within it. The thickness/span ratio is 1:18 (0.055). This is the ‘limit arch’, ensuring that stress will be compressive rather than tensile, and its thickness (compared to span) is the 'limit thickness'. Any thinner and the arch will collapse. In practice, a larger safety margin is advised, such as the middle-third rule: the arch should be three times as thick as it needs to be ( above left). In the 15th-century, Alberti empirically proposed an absolute minimum ratio of 1:15, despite no knowledge of thrust lines.

These principles apply to theoretical arches. A real masonry bridge, however, is a little different because it has weight and substance, walls, decking and backfill. These cause slight deviation of the thrust-line from pure catenary shape, but as long as the arch is thick enough, with a decent margin of error, the structure will be sound. This helps explain why some of the roughly built ancient bridges are still standing today. Of course, live loads such as heavy lorries apply different force-line profiles, but before 1750 the maximum load was dwarfed by the weight of the masonry.
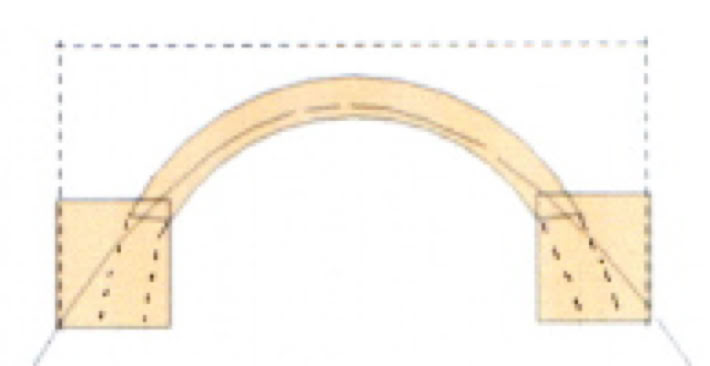
Arches come in all shapes and sizes but this rule generally applies. More often than not it is the skilful use of abutments that assures the stability, and this is especially the case with flat segmental and elliptical arches. Flat arches align better with catenary curves.
Tapered arches, wider at the haunches, are also a good work-around to contain the catenary line.
Page last updated April '25