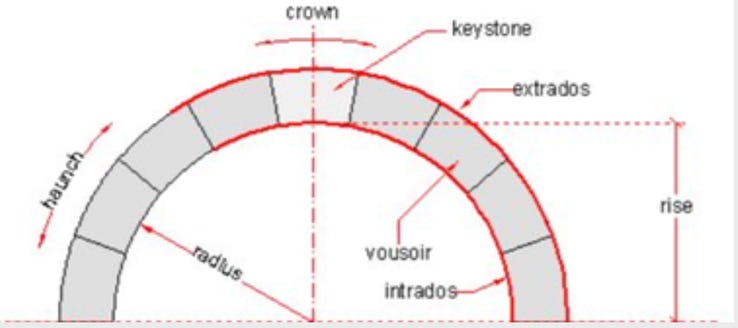
Masonry Arches.
A masonry arch embodies strength from compression, and in practical terms, stone is incompressible. However, stretching or bending ordinary masonry must be avoided because it has very poor tensile strength. It follows that the design must be such that the forces of gravity are directed sideways and downwards within the body of the masonry voussoirs, thus avoiding any significant tension. Once this necessary condition is met, there is no need to consider the relative strength of the masonry material; structural stability has instead become a function of geometry.
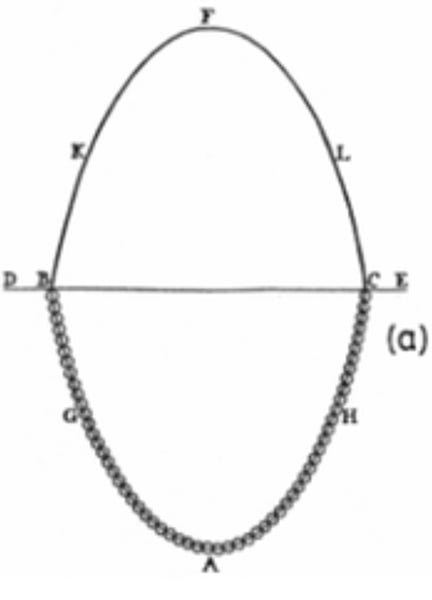
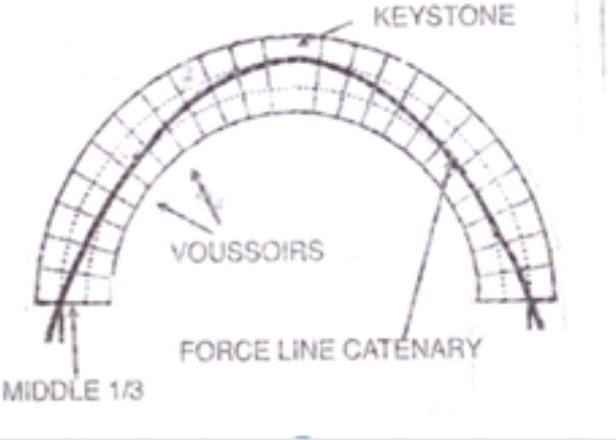
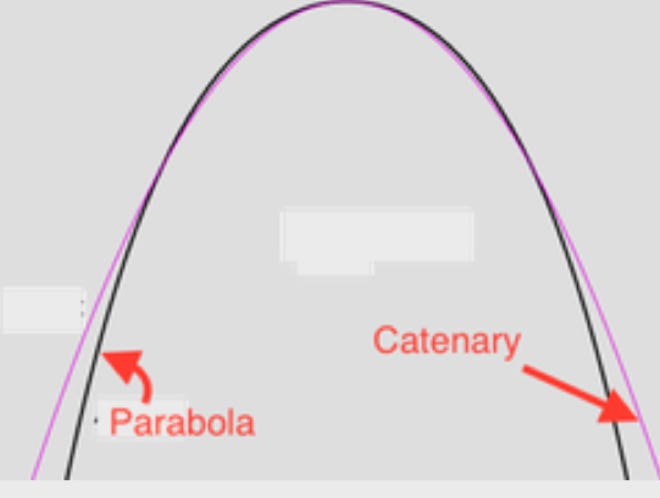
A freestanding arch, with no weight on it, has a gravity force-line in the shape of a catenary: a mathematical function represented by the shape of an inverted hanging chain. Catenaries are a family of curves, just as a hanging chain may be configured to be loose or tight. In theory, an inverted catenary-shaped structure is self-supporting. It would generally seem very sensible to build arches in a catenary shape.
However, other arch shapes are possible, as long as the arch thickness (between in the intrados and the extrados of the arch stones) is wide enough. Clearly, thick voussoirs make this easier to achieve. But if the force-line were to encroach on the edges or lie outside the masonry, then tension would be be expected. This would be followed by collapse of the arch.
All this applies mathematically to a pure theoretical arch. However, a real masonry bridge is a little different because it has weight and substance: decking, parapets, spandrels and infill. This weight on the arch alters the shape of the force-line a little; it changes profile slightly to approach that of a parabola rather than a catenary. The heavier the whole structure, the more parabolic become the force-lines, and most bridges have a force-line somewhere between these two shapes. Today, live-loads such as heavy lorries or locomotives apply point pressures with different force-line profiles; however, before 1750 the maximum live load was dwarfed by the weight of the masonry itself.
Last updated Aug 2022